🚀Introduction
Regression analysis is a widely used technique that allows us to predict the relationship between independent variables (X) and a dependent variable (Y).
The main objective of regression analysis is to model the relationship between X and Y in a way that helps us make accurate predictions for future observations.
However, when the number of independent variables is large, the regression model can become complex, leading to overfitting, which results in poor predictions for new observations.

Above is the equation for linear regression with β1 as the coefficient.
In linear regression, the coefficients are the values that multiply each feature (or predictor) in the model.
The goal is to find the values of the coefficients that minimize the difference between the predicted values and the actual values of the target variable (basically minimizing the errors!).
📈Let's understand overfitting better!
Overfitting is a common problem in machine learning and data analysis. It occurs when a model tries to fit all the information it has, even if some of it doesn't belong.
This results in a model that might perform well on the data it has seen, but it won't be able to make good predictions on new data because it has learned the noise and random fluctuations in the data.
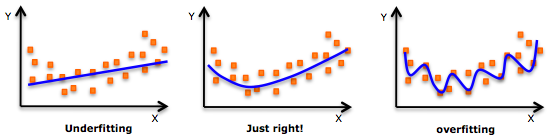
The image above shows a comparison of 3 types of models. Focusing on overfitting, as shown the graph tends to fit all the points given in the data, thus if new data is to be predicted, it may not be able to make the correct guess since it has fitted the training data too well.
To address this issue, we use regularization techniques, such as Lasso and Ridge regression.
Lasso Regression
Least Absolute Shrinkage and Selection Operator
Lasso Regression is a type of regression analysis that helps to prevent overfitting by reducing the magnitude of the coefficients of the features that are not important.
It does this by adding a penalty term. (L1 penalty term)
This penalty term adds a cost to the complexity of the model.
It is proportional to the sum of the absolute values of the coefficients.

The first term in the above equation is themean square errorwhich measures the difference between the actual values and the predicted values of the target variable.
The second term is the**Lasso penalty term, which is proportional to the sum of the absolute values*of the coefficients.*
Ridge Regression
Type of linear regression that uses an L2 penalty term to regularize the model and prevent overfitting.
Ridge penalty term is proportional to the sum of the squares of the coefficients.

The first term is themean square error (MSE).
The second term is the**Ridge penalty term.
🏆Which one's the best?

Let's compare the two!
| Lasso | Ridge |
| The penalty term is equal to the absolute value of the magnitude of the coefficients. | The penalty term is equal to the square of the magnitude of the coefficients. |
| Some of the coefficients are exactly equal to zero. | Coefficients are small, but not necessarily zero. |
| Useful when you have a high number of features and you suspect that only a subset of the features is relevant. | Useful when you have a large number of features and you want to reduce the variance in your model. |
In summary,
Lasso is best used when you have a small number of important features and want to perform feature selection (selecting only certain relevant features thus reducing complexity).
Ridge is best used when you have a large number of features and want to reduce the variance of your model (high variance = overfitting).
Both are the winners!
👩💻Conclusion
In conclusion, regularization is a technique used in linear regression to prevent overfitting and improve the generalization of the model. Lasso and Ridge are two popular regularization methods that add a penalty term to the loss function to discourage the model from assigning too much importance to any one feature.
📚Resources
Learn more about the concepts!
